- Simple, slow
- Bubble sort
- Insertion sort
- Selection sort
- Fast
- Quick sort
- Merge sort
- Heap sort
- O(N)
- Radix sort
정렬 중 이번엔 Merge sort에 대해 다뤄본다.
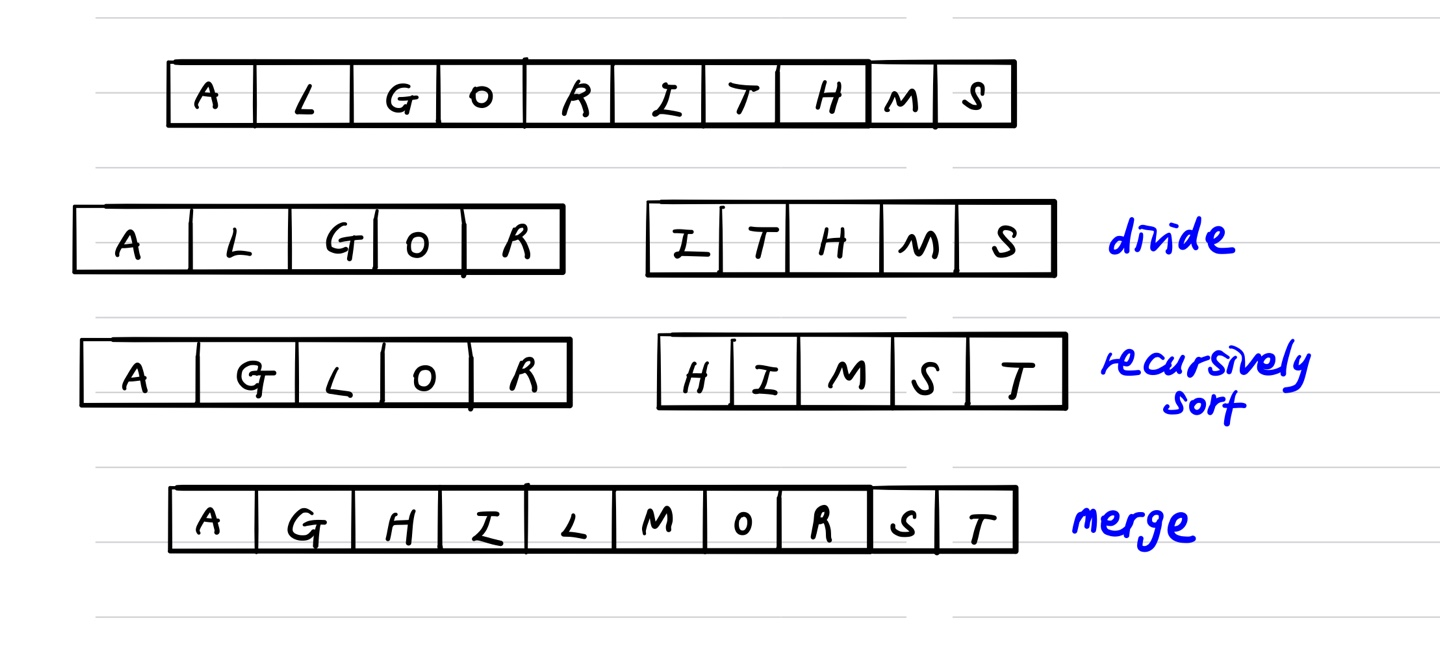
3단계를 거쳐 정렬이 이루어진다.
1) 분할: 해결하고자 하는 문제를 작은 크기의 동일한 문제들로 분할한다.
ex) 최대값을 구할 때, 리스트를 반으로 나누어 각각의 최대값을 구하여, 전체리스트의 최대값을 구하는 것과 비슷하다.
2) 정복: 각각의 작은 문제를 순환적으로 해결한다.
3) 합병: 작은 문제의 해를 합하여 (merge) 원래 문제에 대한 해를 구한다.
늘은 Simple하고 slow한 특성을 갖는 selection sort와 bubbl
mergeSort(A[], p, r) {//A[p...r]을 정렬한다
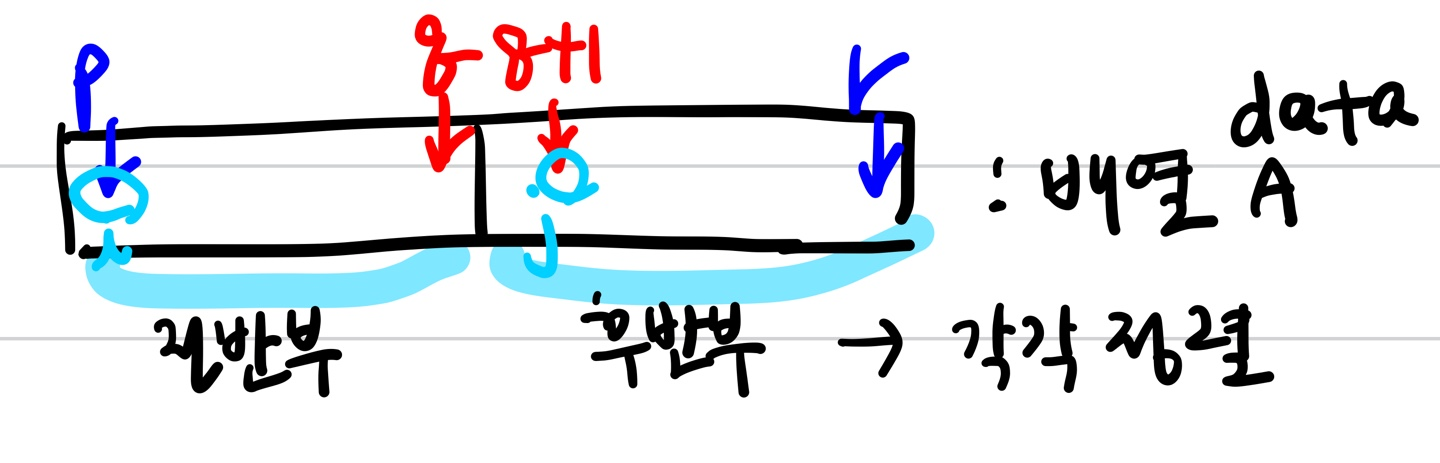
if (p < r){ //p>=r인경우 -> 리스트의 개수가 0 또는 1, 즉 아무것도 안해도 됨
q < -(p + q) / 2; //p,q의 중간 지점 계산
mergeSort(A, p, q);// 전반부 정렬
mergeSort(A, q + 1, r);//후반부 정렬
merge(A, p, q, r);//합병
}
}
merge(A[], p, q, r) {
정렬되어 있는 두 배열 A[p,...,q]와 A[q+1,...,r]을 합하여
정렬된 하나의 배열 A[p,...,r]을 만든다.
}
그렇다면, 정렬된 리스트를 어떠한 방식으로 합병(merge)해야할까?
1) 모두 1개로 쪼개진 리스트로 만들어진 상태라고 가정하자.(initial sequence)
2) i: 1번째 리스트 중 첫번째 값
j: 2번째 리스트 중 첫번째 값
k: 전체 리스트 중 첫번째 값
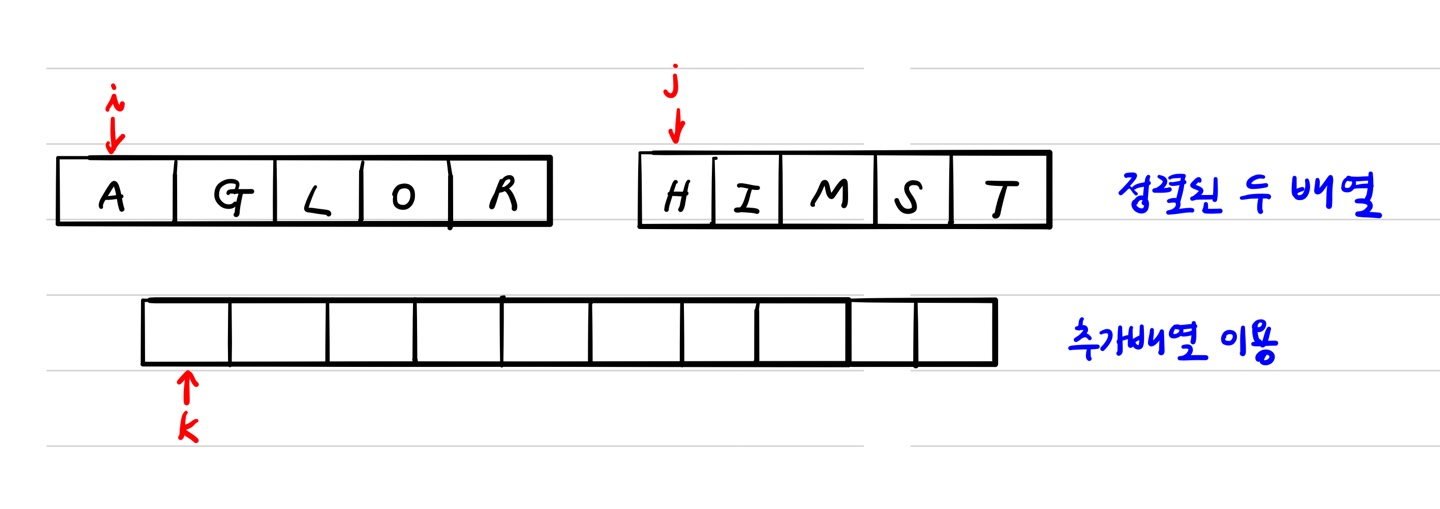
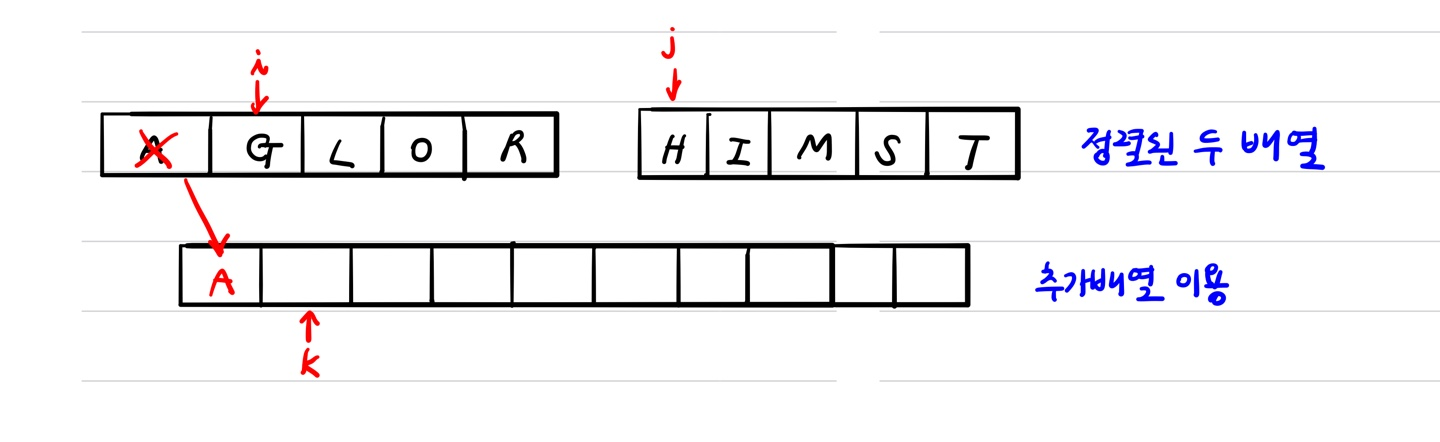
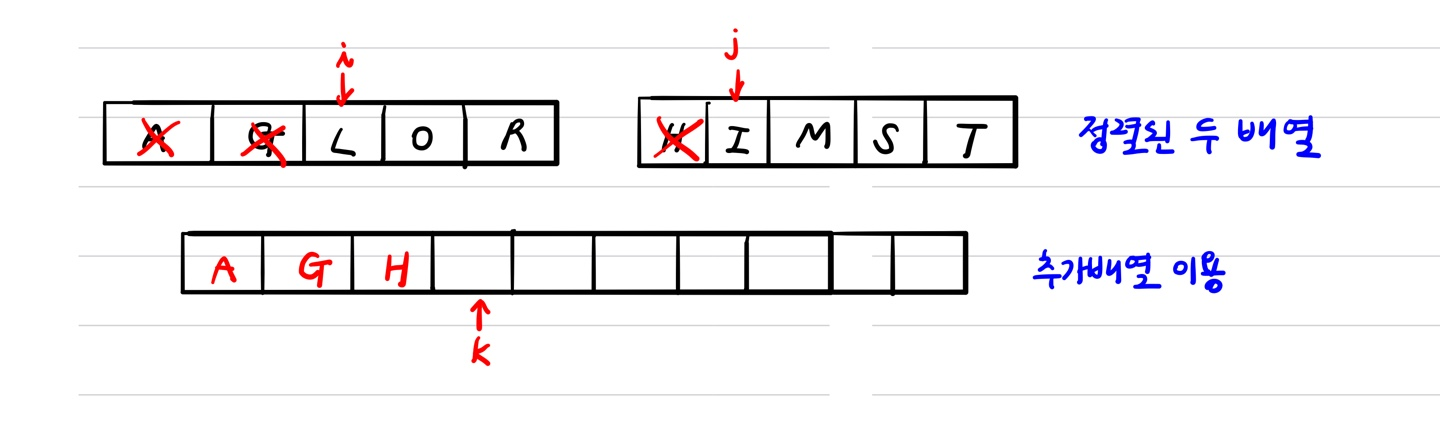
- 위와 같이 i와 j를 이용해 비교하며 새로운 배열의 값 k를 채워나가면 합병 정렬이 완료 된다.
void merge(int data[], int p, int q, int r) {
int i = p, j = q + 1, k = p;
int tmp[data.length()];
while (i <= q && j <= r) {
if (data[i] <= data[j])
tmp[k++] = data[i++];
else
tmp[k++] = data[j++];
}
//쪼개진 리스트 중 하나가 끝에 다다른 경우
while (i <= q)
tmp[k++] = data[i++];
while (j <= r)
tmp[k++] = data[j++];
for (int i = p; i <= r; i++)//tmp리스트를 다시 data리스트로 옮김.
data[i] = tmp[i];
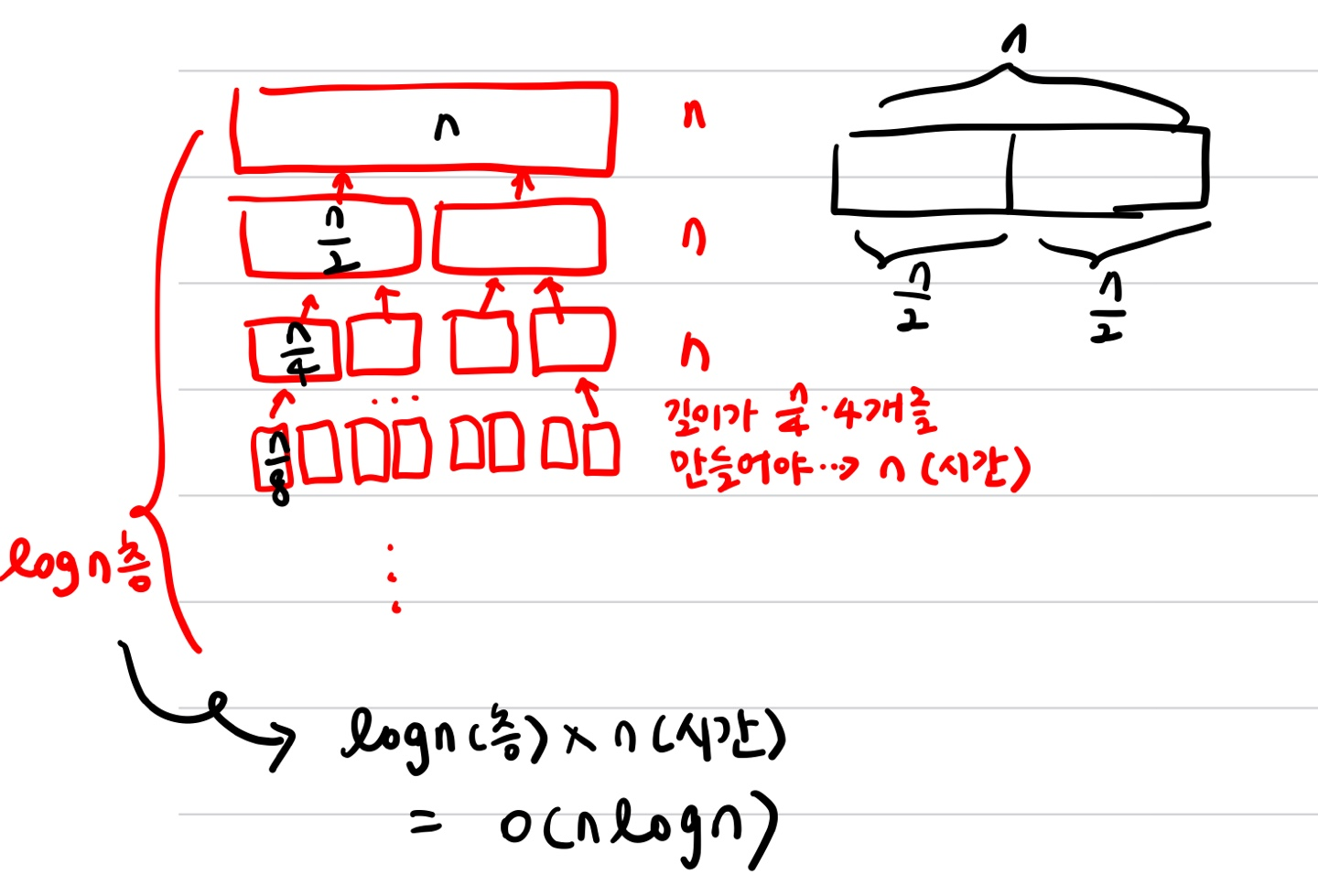
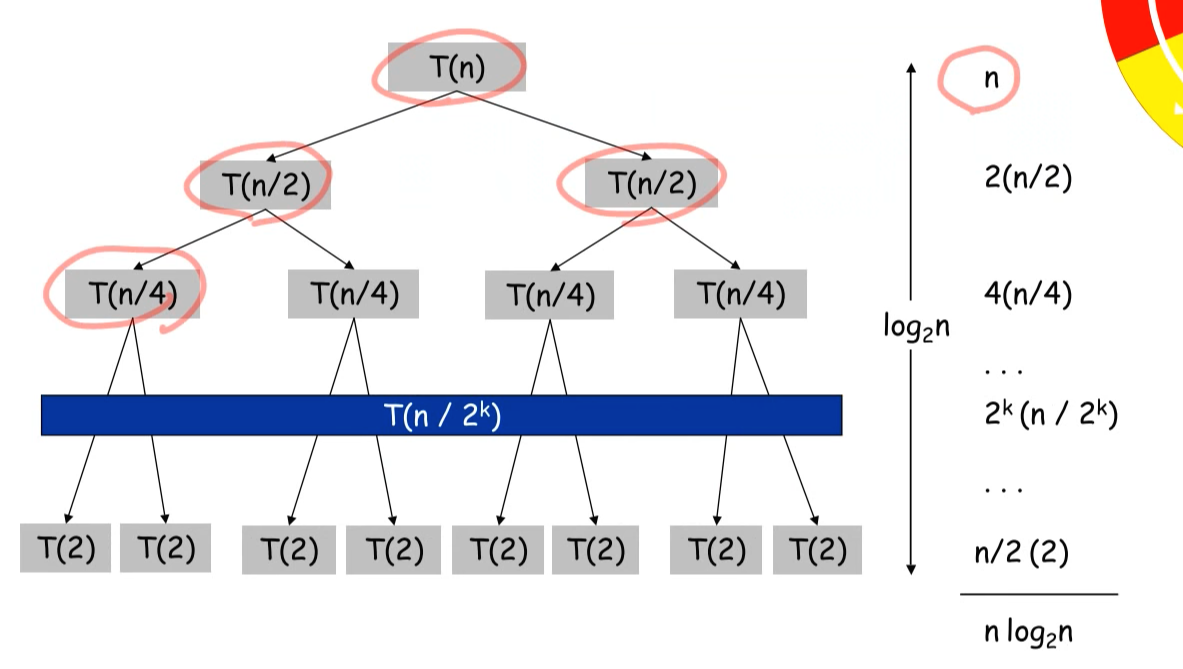
}merge sort의 시간복잡도
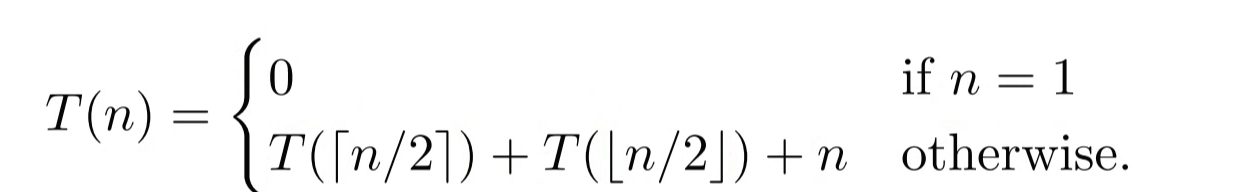
-> T(n)= 2* T(n/2) + n = O(nlogn)
'algorithm' 카테고리의 다른 글
| [ 프로그래머스 | 2022 kako tech internship ] 두 큐 합 같게 만들기 시간초과 해결 (0) | 2023.11.10 |
|---|---|
| C/C++ 헷갈리는 포인터/배열/동적할당 정리 (0) | 2021.04.03 |
| 정렬 알고리즘 종류 (0) | 2020.07.24 |
| 멱집합(Powerset) (0) | 2020.07.23 |
| [recursion 응용] n queens problem (0) | 2020.07.22 |
- Simple, slow
- Bubble sort
- Insertion sort
- Selection sort
- Fast
- Quick sort
- Merge sort
- Heap sort
- O(N)
- Radix sort
정렬 중 이번엔 Merge sort에 대해 다뤄본다.
3단계를 거쳐 정렬이 이루어진다.
1) 분할: 해결하고자 하는 문제를 작은 크기의 동일한 문제들로 분할한다.
ex) 최대값을 구할 때, 리스트를 반으로 나누어 각각의 최대값을 구하여, 전체리스트의 최대값을 구하는 것과 비슷하다.
2) 정복: 각각의 작은 문제를 순환적으로 해결한다.
3) 합병: 작은 문제의 해를 합하여 (merge) 원래 문제에 대한 해를 구한다.
늘은 Simple하고 slow한 특성을 갖는 selection sort와 bubbl


mergeSort(A[], p, r) {//A[p...r]을 정렬한다
if (p < r){ //p>=r인경우 -> 리스트의 개수가 0 또는 1, 즉 아무것도 안해도 됨
q < -(p + q) / 2; //p,q의 중간 지점 계산
mergeSort(A, p, q);// 전반부 정렬
mergeSort(A, q + 1, r);//후반부 정렬
merge(A, p, q, r);//합병
}
}
merge(A[], p, q, r) {
정렬되어 있는 두 배열 A[p,...,q]와 A[q+1,...,r]을 합하여
정렬된 하나의 배열 A[p,...,r]을 만든다.
}
그렇다면, 정렬된 리스트를 어떠한 방식으로 합병(merge)해야할까?
1) 모두 1개로 쪼개진 리스트로 만들어진 상태라고 가정하자.(initial sequence)
2) i: 1번째 리스트 중 첫번째 값
j: 2번째 리스트 중 첫번째 값
k: 전체 리스트 중 첫번째 값



- 위와 같이 i와 j를 이용해 비교하며 새로운 배열의 값 k를 채워나가면 합병 정렬이 완료 된다.
void merge(int data[], int p, int q, int r) {
int i = p, j = q + 1, k = p;
int tmp[data.length()];
while (i <= q && j <= r) {
if (data[i] <= data[j])
tmp[k++] = data[i++];
else
tmp[k++] = data[j++];
}
//쪼개진 리스트 중 하나가 끝에 다다른 경우
while (i <= q)
tmp[k++] = data[i++];
while (j <= r)
tmp[k++] = data[j++];
for (int i = p; i <= r; i++)//tmp리스트를 다시 data리스트로 옮김.
data[i] = tmp[i];
}merge sort의 시간복잡도
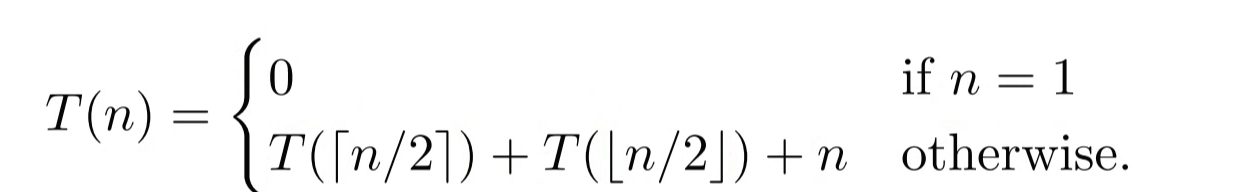
-> T(n)= 2* T(n/2) + n = O(nlogn)


'algorithm' 카테고리의 다른 글
| [ 프로그래머스 | 2022 kako tech internship ] 두 큐 합 같게 만들기 시간초과 해결 (0) | 2023.11.10 |
|---|---|
| C/C++ 헷갈리는 포인터/배열/동적할당 정리 (0) | 2021.04.03 |
| 정렬 알고리즘 종류 (0) | 2020.07.24 |
| 멱집합(Powerset) (0) | 2020.07.23 |
| [recursion 응용] n queens problem (0) | 2020.07.22 |
